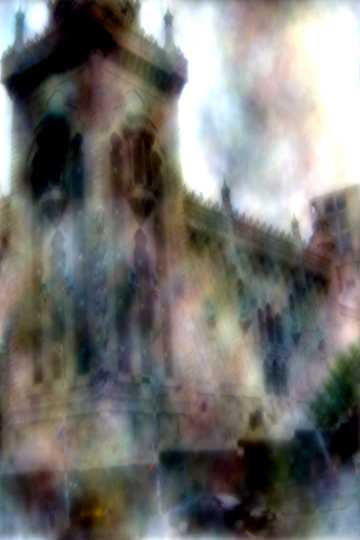
Fourier

This page tells you about an experiment with Fourier analisys applied on pictures. I started it as a attempt to understand why modern achitecture is so awefully ugly. And I came to the conclusion that it must be the stupid and ugly repetition of a simple patern. When looking at an old church you will find structures of many sizes, and on every scale the building is interesting. In modern buildings you will find one simple patern that is repeated time and again. In terms of Fourier analysis this means a small number of frequencies dominate. I thought: what if you would apply Fourier analysis and maintain the phase of each component of the analysis, but change the amplitude of the component to a fixed patern? So I made a program that allowed me to do so, and here are the results. The program calculates the Fourier analysis and then changes the amplitude of each component to a certain pattern.

The results are often surprising, giving the picture a impressionistic character. Note that simple repetitions are significantly suppressed. Like in the picture with blinds or bricks.

With this program you can choose the frequency patern in the figure. The choises for frequency distributions are:

amplitude = 1/sqrt( (f ²+const ²)
amplitude = 1/(f ² +const ²)
amplitude = 1/ sqrt(f ²+const ²) ³
amplitude = exp( -f/const)
amplitude = constant
amplitude = raised to the power of const ((De-)amplification)

The formulea and constant can be chosen. Most pictures below are modified using the second formulea and constant set to 2. These settings make low frequencies dominate. The pictures with sharp changes use the "amplitude = constant" formulea.

Warning

Warning:

It is time consuming, the time needed increases with the square of the area: a picture of 100 x 100 pixels took my Intel Core CPU 2.4GHz 20 minutes for a 640 x 480 picture Fourier transform and 25 min. for a reverse Fourier transform, a picture of double that width and height (4 times bigger area) will take about 16 times as much.

Because this is a slow process I made the possibility to create a queue of modifications, and let the computer generate pictures and store them on your disk. So you can let the computer create Fourier modifications when you don't need it. The last part of this page has larger pictures.

The program needs disk space to store the Fourier transform, (.ft file) which will be quite large, 16 x 3 times the pixel size. So almost 15MByte in the case of a 640 x 480 picture. This file will not be deleted automatically since it usually takes a lot of time to make it, and it will be used again when you restart the program with the same picture file. You can make the program delete it after it closes, by chosing so in the menu item "Fourier & Colors". When you drag and drop the .ft file in the Fourier program it will do a reverse Fourier transform and re-create the picture. This will, as mentioned earlier, take some time.

Since the version of 20-3-2016 this program can handle both .JPG and .BMP formats. Also copy/paste, and drag and drop work.

Download Fourier.exe















	Here are two versions of a Monet: Upper left is the original, upper right has been modified with the 1/(f+c)², the left one has been modified with 1/(f+c).

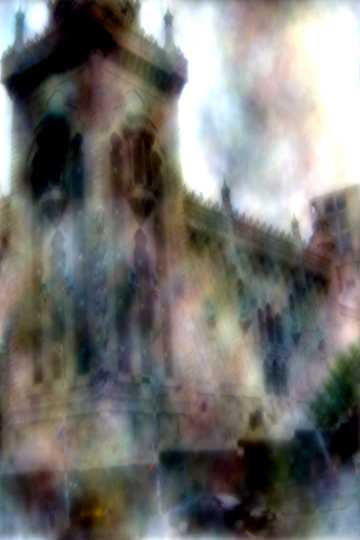Here you will find some experiments with buildings. Notice when you use amplification of the frequencies the buildings will look more modern.

Original	Option: Amplification 1.2	Option: Amplification 1.5
Option Amplification 0.8	Option Amplification 0.5	Option: Amplification 2
Option: 1/R, parameter 1	Option: 1/R², parameter 1
Original	Option: amplification 1.5	Option Amplification 0.7
Option 1/R parameter 1	Option 1/R² parameter 2