

Pentagons and the Golden Section.
Tiling with regular polygons
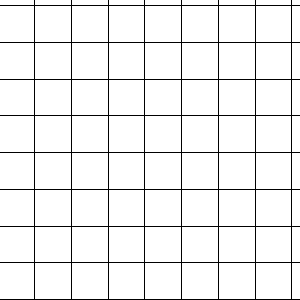
With regular polygons like triangles and squares, and hexagons one can cover a plane completely. We have all seen figures like this. A plane covered with triangles can be constructed with parallel lines with equal distances. Add the same pattern rotated with 120º and 240º, and you will get plane filled with triangles like fig. 1. Each side of each triangle coincides with one of the lines. With squares it is even simpler: you need just two patterns of parallel lines, rotated 90º with respect to each other. See fig. 2. The line pattern of hexagons is the same as for triangles (Fig 3).
 |
 |
 |
| Fig. 1. Tiling with triangles. | Fig. 2. Tiling with squares. | Fig. 3. Tiling with hexagons. |
.
Pentagons and Tiling?
Can you do the same with pentagons? Yes and no. You can't cover a plane completely with regular pentagons, but you can find a lot of pentagons in a pattern of lines that is constructed in the same way as mentioned before. You do need some changes. The patterns of parallel lines should of course have an angle of 72º in respect of one another. The big difference is the fact the parallel lines are not equally spaced any more. See fig 4. The distances between two consecutive lines can be "Big" or "Small". The ratio of the "Big" distance and "Small" distance is φ. φ is the so-called Golden Section. See box 1. The distances between the lines do not change in a regular way. The ratio of the number of "Big" and "Small" distances is approaches φ. And since φ is not an element of N, Z, or Q, there can not be regularity.
 |
 |
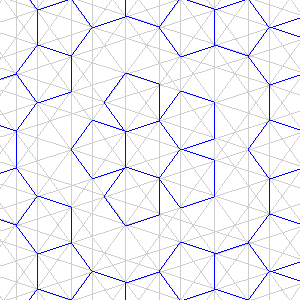 |
| Fig. 4. Pattern of lines for the tiling with pentagons. The normal of this pattern has a 0º angle. | Fig. 5. Pattern of lines like Fig. 4, but now also rotated 72º, 144º, 216º, 288º. | Fig. 6. Pentagons drawn in this pattern of lines. Notice that each pentagons (drawn in blue) has an inscribed star. |
Pentagons in this pattern of parallel lines.
We have just defined a pattern of five groups of parallel lines, but how to find the pentagons is this figure? Of course you can write a computer program and make it calculate very accurately where the intersections are, and make it check if they make a regular pentagon. This does not satisfy a true mathematician. He does not want to know it accurately, but exact. And in this case it can be done. If you have defined it all nicely, it appears you can express the distance of the lines that form a pentagon (the sides of the pentagon are a part of these lines) to the origin in an integer plus an integer times φ. This fact makes calculating and comparing it, much faster and exact. How one can calculate like this is explained in box 2.
The Series for the line distances.
I did already tell you something about the line distances, namely that the ratio of the number of "Big" distances and the number of "Small" distances is φ. Now you can make a series of B's (="Big" distances) and S's (="Small" distances) by staying close to this observation. You just have to calculate the number of B's divided by the number of S's. If the result is bigger than φ, you add a "S", otherwise you add a "B".
Algorithm: Series := "B" index =1; NS = 0; (* = number of "S" *) NB = 1; (* = number of "B" *) REPEAT IF (NB>NS*φ) THEN Series[ index] := "S"; NS = NS+1; ELSE Series[ index] := "B"; NB = NB+1; END; index := index+1; UNTIL (index >= MaxIndex); You will get a series like: BSBSBBSBSBBSBBSBSBBSBSBBSBBSBSBBSBBSBSBBSBSBBSBBS...
The construction of the figure with pentagons.
Constructing the figure with pentagons you start with a normal of 0º and you start drawing lines perpendicular on the normal. The starting point (=offset) on the normal is shown in Fig. 7. The distances between these line vary between "Big" (="B" = φ +2) and "Small" (="S"= 2φ-1). The offset must be expressed in an integer and an integer times φ: offset = n + mf, with n and m an integer. This system is to be repeated for a normal of 72º, 144º, ect.. Using this construction you will find many pentagons with inscribed star if m/n ≈ φ. For each value of n there are 4 to 5 consecutive values for φ that will give pentagons in the figure. So with the most values of m you will not find any pentagons.
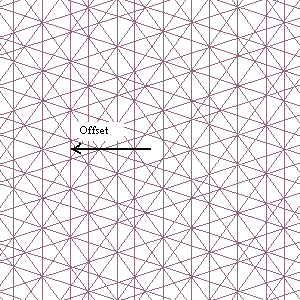 |
| Fig. 7. The offset of the pattern of lines. The same pattern of lines is rotated 72º each time. For reasons of clarity only a few lines have been drawn. |
With the program that you can download you can change the offset (= change the value of n and m). The program will only try to find pentagons with inscribed star. If you leave out this last criterion you will find a lot of overlapping pentagons. The program will find pentagons in the following way: With each intersection of two lines one can determine where a possible pentagon can be found. Then you check if the sides of this pentagon coincide with the lines of the pattern of lines. Since the distances of both the sides of the pentagon and the lines of the earlier defined pattern of lines can be expressed as an integer and integer times φ, the comparison is simple and accurate.
Self-Similarity and Pentagons.
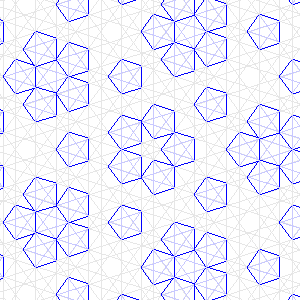
If you have a closer look at the figures 8 and 9 you will find that the same pattern of lines have a bigger version of the pentagons with star. This was more or less to be expected since the big and small distances between the lines have a ratio of φ, and the ratio of the number of "Big" and "Small" distances is also φ. You can define a bigger order by stating B1 = B0+S0; S1 = B0; With B0 as "Big" distance (=φ), and S0 as "Small" distance (=1) of order zero: B1 and S1 (= the "Big" and "Small" distances of order 1): B1 =1+φ; S1 = φ; B0/S0 = B1/S1 = φ; The ratio of the numbers of B's and S's remain the same.
 |
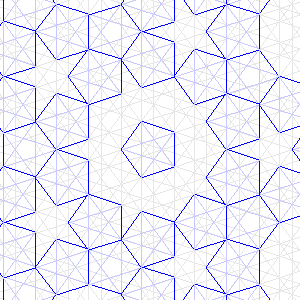 |
| Fig. 8. Pattern of lines with small pentagons with inscribes star. | Fig. 9. The same pattern of lines as in fig. 8 but now with bigger pentagons with inscribed star. |
This can also be derived from the series of B's and S's. When one replaces an "B" by an "S", and an "SB" by an "B" one gets the same series. Only the first two elements from the series are an exception. One can also do the opposite: replace an "S" by an "B", and an "B" by "SB". With this system you can derive the series from itself.
Algorithm: Series := "BS"; index := 1; Length :=2; REPEAT IF (Series[ index] = "S") THEN AddString( Series, "B"); Length := Length +1; ELSE AddString( Series, "SB"); Length := Length +2; END; index := index + 1; UNTIL (Length >= MaxIndex);
This algorithm looks like the Turing machine. It will give the very same series as the one previously described. The phenomenon of a pattern remaining the same under (de) magnification is called self-similarity. See box 3.
Box 1. The Golden Section.
The Golden Section. The Golden Section is the ratio that equals:
big length big + small length
φ = -------------- = -----------------------
small length big length
It is a ratio often used in arts because it gives a nice division, and it was already known with the classical Greeks. From the definition you can calculate φ = ½*(1+√5).
And further it holds that:
1/φ = φ-1 ; φ² = φ+1 cos( 36º) = φ/2; cos( 72º)
= 1/(2φ)
And for the fanatics: 2*sinh( ln( φ) ) = 1.
φ is also the limit of two successive elements of the Fibonacci series: F( n+1) = F(n) + F(n-1): 1, 1, 2, 3, 5, 8, 13... φ = Limit (F(n+1)/F(n)) with n approaching infinity. An other way to link the Fibonacci series and φ is to divide constantly by φ: 1/φ = φ-1; (φ-1)/φ = 2-φ; (2-φ)/φ = 2φ-3 ... = F( n)φ - F(n+1) This series will converge to zero because you keep on dividing by a number bigger than 1.
Box 2. Calculating with the Golden Section.
One can calculate with the Golden Section in a way similar to the way one calculates with complex numbers. When calculating with complex numbers, one calculates with a real and an imaginary number. In case one calculates with Golden Section, one calculates with an integer number and an integer number times φ.
Given Z = n + m* φ
Add: Z1 + Z2 = (n1+n2) + (m1+m2)*φ
Multiply: Z1 * Z2 = (n1*n2 +m1*m2) + (n1*m2 + n2*m1 + m1*m2)*φ
Dividing by φ: Z/φ = (n-m) + m* φ
Dividing in general:
(n+m) - m* φ
1/Z = n2+m2*φ= --------------
(n² + n*m -m²)
In general the resulting n2 and m2 will be no integers, but elements of Q.
Box 3. Self-Similarity.
Self-similarity is the case that a (de) magnification does not change the figure. For instance the following figure: fig. 10.
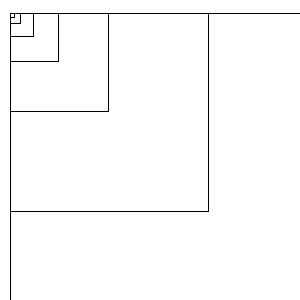 |
| Fig. 10. Self-similarity. This figure does not change if it is (de)magnified twice. |
Dimensions of a regular pentagon.
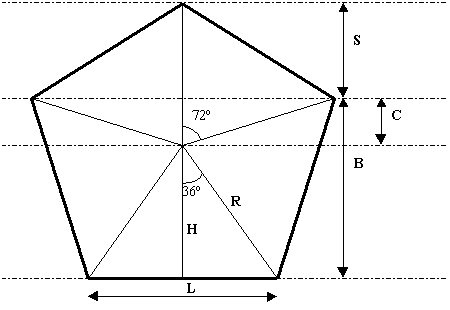
Dimension in a pentagon.
L = 2*R*sin(36º) C = R*cos(72º) H = R*cos( 36º) S = R-C= R*(1-cos(72º) ) B = H + C = R*(cos(36º)+cos(72º)) cos( 36º) = φ/2 cos( 72º) = 1/(2φ) == > C =R/(2φ) S= R*(1-1/(2φ)) = R*(1-½*(φ-1) ) = ½*R*(3-φ) B= ½*R*( φ+1/φ) = ½*R*(1+ 2φ) With R = 2φ: C = 1 S = -1+2φ B = 2 + φ The program that you can download changes the start position with steps of 1 and φ. cos( 36º) = φ/2 is easiest to prove with cos(2*36º+½*36º)=0 ==> cos(2*36º)*cos(½*36º)=sin(2*36º)*sin(½*36º) ==> (2*cos(36º)^2-1)*cos(½*36º)=2*sin(36º)*cos(36º)*sin(½*36º)
Some samples:




Version 2.1 available: this one can also draw solid pentagons.
Some samples:




